Paul Erdos: Matematikawan Keliling Sedunia

Pil amfetamin adalah kesukaannya. Tapi, jasanya, besar dalam dunia matematik.

Sudah senja, dan efek pil amfetamin yang ditelan Paul Erdos sewaktu makan siang di AT&T Bell Laboratories, kelihatannya mulai menurun. Sejak jam 5 pagi, ia sudah berkeliaran, keluar masuk setiap kantor laboratorium Bell, menelpon kolega di seberang lautan. Satu-satunya yang dikeluhkannya, cuma umurnya, yang 71 tahun.

Cuma, umur ini jangan sangka akan membuatnya gegabah mengundurkan diri. Ia tetap masih satu-satunya matematikawan keliling di dunia. Punya rumah? Tak terbayang olehnya. Bahkan tak terbayang olehnya untuk memiliki apapun keciali yang muat di dua kopor kecilnya. Itu saja. Minggu lalu, ia berada di berbagai kota AS. Malam ini, ia ke Kanada, ilan terus ke Israel, Jerman, Hongaria, Australia, tiada henti. “Banyak waktu untuk beristirahat di kuburan,” katanya.

Tapi, saat ini, berjalan di lorong dengan sandal butut dan jaket bergaris abadinya, kepala menunduk, jenggot 2 hari belum dicukur, ia memang tampak lelah. “Ron,” katanya, setelah berhenti di salah satu pintu. “Kita harus cepat pulang. Saya perlu waktu untuk mengepak barang.” “Tidak, Paul, saya yang perlu waktu untuk mengepak barang anda,” jawab si Ron. Memang, Ronald Graham, yang sehari-harinya kepala sekitar 70 matematikawan yang berada di lab Bell, setiap kedatangan Erdos, berkewajiban melayaninya. Termasuk mengantarnya kemana saja perlu, dan mengurusi semua keperluannya dari cuci pakaian sampai ke dokter.

Bukan, Erdos bukannya minta diservis semacam ini. Cuma, ia memang perlu dibantu yang ada hubungannya dengan keduniawian. Pernah ia ke Jepang, dari Amerika, dengan cuma membawa Rp. 50.000 di kantongnya. “Tak perlu takut,” katanya kemudian. “Saya punya teman di mana-mana.” Bahkan dia pun tidak mengurusi keuangannya sendiri. Si Graham itulah yang mendepositokan ceknya, dan membayar tagihannya.

Tapi. Erdos punya cara tersendiri untuk membayar hutang budinya. Dia tak banyak uang. memang, karena tak punya pekerjaan tetap, hanya honor dari ceramah dan tanggungan dari departemen-departemen matematika yang dikunjunnya. Tapi. bila ada matematikawan atau rnahasiswa yang perlu uang, dia pasti memberinya. Ia menganggapnya sebagai pinjaman yang boleh atau tidak dibayar kembali. Tahun lalu, misalnya, sewaktu memenangkan Rp. 50 juta lebih Hadiah Wolf yang bergengsi itu, dia hanya menyimpan sekitar Rp 750 ribu untuk dirinya. Selebihnya? Dibagikannya untuk saudarasaudaranya, dan untuk dana beasiswa mengenang ibunya. Dan ada satu hadiah lagi yang lebih penting: masuk dalam kantor seorang matematikawan dan berkata, “Otak saya terbuka”. Itu, artinya, ia sudah siap melanjutkan kerja yang terhenti pada kunjungan sebelumnya. Banyak matematikawan yang hidup menyendiri untuk memecahkan satu persoalan. Tapi Erdos, sebaliknya, bekerja dengan kolega di seluruh dunia, menyempatkan waktu untuk lusinan masalah dari teori angka sampai topologi. Ia menulis 1500 surat setiap tahun. Matematikawan kelas satu, biasanya, mempublikasikan sekitar 50-100 makalah sepanjang hidupnya. Erdos telah mempublikasikan lebih dari 1000. Ia, mungkin, adalah matematikawan hidup paling produktif, bahkan sepanjang sejarah. Inilah satu sebab kenapa matematikawan di seluruh benua menganggap tanggungjawab mereka untuk menjaganya. Mereka memandangnya sebagai bakti kepada matematika.

Yang menjadi pikiran para matematikawan, kini, adalah kemungkinan tak mampu lagi Erdos mengunjungi tempat mereka. Itulah, sebabnya, banyak yang menasihatinya supaya mengendurkan kebiasaannya bekerja 16— 20 jam setiap hari. Beberapa tahun lalu, Graham juga berusaha menghentikan kebiasaannya yang lain: menelan pil amfetamin! Ia mulai meminumnya setiap hari setelah kematian ibunya, tahun 1971, diberi dokter sebagai obat antidepresan. Dia membandingkan pil ini seperti kopi kuat, dan malah berkata: “Matematikawan adalah mesin yang mengubah kopi menjadi teori.” Tapi, Graham kuatir, dan menawarkan Erdos sekitar Rp. 500 ribu kalau mau menghentikan kebiasaannya sebulan saja. Erdos setuju tantangan ini, meskipun tak senang. Ia malah berkata, “Dulu, kalau saya memandang kertas kosong, otak saya menjadi penuh dengan ide. Kini, yang saya lihat cuma kertas kosong saja.” Ia bahkan memperingatkan Graham: “Anda menghambat kemajuan matematika.” Akhirnya, setelah sebulan dan memenangkan Rp. 500 ribu itu, ia kernbali melanjutkan kebiasaannya, minum amfetamin .

Senin di Montreal. Erdos, seperti biasanya, mengarungi ruang-ruang akademi. Enam hari setelah meninggalkan lab Bell, ia menyelesaikan makalah dengan seorang matematikawan Israel di MIT. Malam kemarin, di Montreal, ia kembali mengerjakan perincian pem-buatan makalah lain dengan seorang matematikawan India. Kini, ia sedang berceloteh riatig dengan sekumpulan matematikawan yang mengikutinya. Berbahasa Hongaria dengan yang satu, Prancis dengan yang lain, Inggris dengan lainnya —tapi selalu dengan gaya bahasanya yang tersendiri.

Tersendiri? Memang. Coba, misalnya, kata-kata begini: “Bagaimana dengan epsilon anda?” atau S.F.” nampaknya menginginkan saya sakit.” Apa yang dimaksud dengan epsilon dan S.P. itu? Epsilon, huruf Yunani yang dipakai matematikawan untuk kuantitas kecil, adalah istilah Erdos untuk anak. S.F. itu, Supreme Fascist (Fasis Tertinggi), yang maksudnya Tuhan. Ketika berumur 60 tahun,
tanda tangannya mulai ditambah dengan singkatan L.D. Artinya? Living Dead, atau Mayat Hidup. Sewaktu mendengar bahwa umur bumi adalah 4,5 milyar tahun, ia teringat dulu waktu semasih kecil para geolog memperkirakannya 2 milyar tahun. Jadi, ia mulai melakukan semacam ceramah otobiografis berjudul, 2,5 Milyar Tahun Pertemaku dalam Matematik.

Sesuatu yang lndah
Kelihatannya aneh, paling tidak tak adil, kalau orang awam tidak mengenal apa yang dikerjakan Erdos selama 50 tahun belakangan. Coba ambil contoh bidang ilmu lainnya, bahkan yang paling muskil dari astrofisika, orang awam paling tidak tahulah tentang perkembangan terakhirnya. Bisakah orang dibilang terpelajar, misalnya , kalau belum pernah mendengar Big Bang atau DNA? Tapi, biar diarpelajar drarn. bidang matematik, orang merasa cukup mengenal sedikit ilmu ukur ruang dari zaman Yunani kuno, dan sedikit aljabar dari abad pertengahan. Sedikit ingin tahu tentang kalkulus, dianggap terlalu, padahal itu dikembangkan di abad 17 . Bagi orang awam, matematik telah berakhir 300 tahun lalu.

Para matematikawan, tentu , menyayangkan keadaan begini. Kata mereka, misalnya, matematikawan yang bekerja kini sama saja banyaknya dengan fisikawan. Bahwa perubahan paling revolusioner dalam sejarah matematika terjadi di abad ini. Matematika masih tetap “Raja Ilmu Pengetahuan”, masih tetap dianggap kreasi paling tinggi dan paling murni dari otak manusia.

Jadi, kenapa diabaikan, Mungkin, karena terlalu rumit (matematikawan memakai istilah dan simbol tertentu jauh sebelum ilmuwan lainnya), dan tak mengenal kompromi (bisa memecahkan masalah, atau tidak). Tapi, mungkin, alasan utama adalah karena matematikawan, tidak seperti para ahli fisika dan biologi, tidak pernah berprasangka ingin menjelaskan alam semesta fisik ini. Cara hidup Erdos itu mencerminkan kerja matematikawan murni: sama sekali tidak memperdulikan dunia nyata. Tulis G.H. Hardy, matematikawan Inggris, “Saya tak pernah melakukan satupun yang berguna. Tak ada penemuan saya yang akan, atau kemungkinan akan, langsung atau iak langsung, mengubah dunia ini.” Judul bukunya, A Mathematician’s Apology. Sebenarnya, ia jauh dari meminta maaf (apology). Ia adalah matematikawan murni karena bangga akan ketiadagunaannya!

Namun, Hardy ternyata salah tentang kerjanya sendiri. Spesialisasinya teori angka (number theory), bidang yang selama 2000 tahun dianggap tak praktis dan kelihatannya akan tetap begitu setelah ia meninggal 1947 lalu. Tapi, dalam kurun waktu dekade terakhir, teori angka ternyata sangat penting untuk membuat dan memecahkan kode pengiriman informasi antar komputer. Jadi, Hardy secara tak langsung besar jasanya dalam kehidupan kita saat ini, dari dunia mata-mata sampai ke transaksi uang.

Itulah uniknya paradoks matematik. Tak perduli betapa acuhnya matematikawan terhadap dunia nyata, mereka selalu menghasilkan alat terbaik untuk memahaminya. Orang Yunani kuno, misalnya, bertekad mempelajari (karena alasan yang tak jelas) sebuah kurva yang disebut elips —2000 tahun kemudian, para astronom menemukan bahwa begitulah cara planet mengedari matahari. Lagi, karena alasan tak jelas, seorang matematikawan Jerman 1854, Bernhard Riemann, ingin tahu apa yang terjadi kalau ia membuang satu dalil keramat ilmu ukur bidang Euclid. Kemudian, ia membuat satu sistem geometri sekitar asumsi aneh bahwa tak mungkin untuk membuat 2 garis yang saling seiaiar. Geometrinya mengganti bidang Euclid dengan sesuatu yang abstrak aneh —60 tahun kemudian, Einstein mengumumkan bahwa begitulah bentuk alam semesta.

Paul Erdos terlalu sibuk bekerja dengan teorinya untuk sempat memikirkan betapa pentingnya pekerjaannya. Orang lain, mungkin, bisa mene-rangkan kegunaan aplikasi pekerjaannya, tapi tidak Erdos. Ia, bahkan, tak bisa menunjuk satu pun hasil praktis dari 1000 makalahnya itu. Kebanyakan karyanya termasuk dalam kategori yang disebut discrete mathematics, yang berurusan dengan sekum-pulan pokok yang berbeda —sekumpulan 20 titik dalam sebuah bidang, misalnya, atau serangkaian bilangan bulat positif. (Kategori lain dalam matematilc modern adalah “berkesinambungan” (continous), karena berurusan dengan struktur ruang —seperti grafik atau parabola atau lingkaran— yang tak bisa dipecahkan menjadi komponen diskrit). Erdos mulai dengan salah satu bentuk matematik diskrit paling tua, teori angka, yang meneliti sifat bilangan bulat —apakah, misalnya, sebuah angka bisa dibagi sama dengan angka yang lebih kecil. Angka seperti 11 atau 29 disebut prima karena tak dapat dibagi oleh angka yang lebih kecil kecuali 1. Makalah Erdos pertama, ditulis ketika baru 18 tahun, membuktikan bahwa selalu ada angka prima antara setiap bilarlan bulat n dan 2n.

Tahun 1930, Erdos menggauli bidang yang waktu itu belum jelas —kombinatorik. Karena sebagian kerja pionirnya inilah, mungkin, kombinatorik kini menjadi salah satu bidang matematika yang paling cepat ber-kembang. Seperti anda sudah tebak, ia berurusan dengan kombinasi —dengan cara untuk mengatur dan mengklasifikasikan anggota dari satu rangkaian. Latihan kombinatorik umum adalah “masalah pengepakan”.

Andaikan anda mempunyai
a) persediaan ubin persegi empat tak terbatas yang sisinya masing-masing 1 cm.
b) tempat parkir sangat luas yang perlu diubini; dan
c) kemauan degil untuk menutupi sebanyak mungkin tempat parkir itu tanpa ada ubin yang saling tumpang tindih.

Sekarang, bagaimana anda mengatur ubin itu? Mulailah dengan keadaan sederhana: tempat parkir yang persis persegi empat berukuran 100.000 cm setiap sisi. Mulailah dari satu ujung, dan kerjakan ubin itu dengan deretan 100.000 ubin yang rapih. 10 milyar ubin kemudian, selesailah tugas anda.

Tapi, andaikan setelah selesai, anda menemukan bahwa tempat parkir itu ternyata luasnya 100.000,1 cm pada setiap sisi. Jadi ada tempat yang belum terubini; selebar 1/10 cm. Apa yang harus anda lakukan? Mungkin anda akan bilang, “Yah, biar saja. Capai!” Tapi tidak Erdos, Graham, dan Hugh Montgomery dari Universitas Michigan yang menemukan cara terbaik untuk meletakkan ubin itu. Mereka menghitung persis bagaimana meletakkannya sehingga terjadi ruangan yang bisa diisi ubin lagi. Memang terdapat ruang ama t kecil antar ubin itu, tapi 6000 ubin bisa ditambahkan.

Erdos tak bisa menjelaskan kenapa ia memikirkan hal-hal semacam ini. Matematikawan, yang begitu persis mendefinisikan istilah kerja mereka, biasanya tak tahu bagaimana menerangkan arti dari kerja mereka. Bagi seorang matematikawan, tempat parkir angan-angan Erdos itu mencerminkan sesuatu yang lebih dalam —pokoknya, mencerminkan sesuatu yang menurut Bertrand Russell, sesuatu yang “murni tiada tara” dan memiliki “keindahan agung mencekam”. Atau, seperti kata Graham, “Cara Erdos berusaha mencari kebenaran.”

Mungkin, cara terbaik untuk menghargai kesadaran matematikawan ini, adalah dengan melihat prestasi Erdos paling terkenal, bukti dari 129jj Angka Prima. Menurut teori, jumlah angka prima yang berada di antara 0 dan n adalah sebanding dengan n dibagi logaritma natural n. Erdos dan Atle Selberg membuktikannya tahun 1949 — setengah abad setelah pembuktian sebelumnya. Jadi, apa istimewanya bukti Erdos itu? Tidak seperti bukti asli tahun 1896 dulu , ia tidak memakai akar dari -1 (yang sering disebut angka angka imajiner). Bukti Erdos, jadi, adalah bukti “elementer”. Ini mengagumkan matematikawan di seluruh dunia karena lebih dasar, lebih murni. “Bukti itu sendiri tidak mengubah apa-apa,” kata Erdos, “Cuma bukti yang bagus.” Cukup, ‘kan?

Lain Dari yang Lain
Erdos mulai tertarik dengan matematik tahun 1917, ketika masih berusia 4.tahun. Ia masih belum bisa menulis angka, jadi perhitungan yang dilakukannya terbatas di dalam otak saja. “Saya sudah biasa mengalikan angka-angka berdigit 3 atau 4 dalam otak,” kenangnya. Tapi, ia tidak menganggap ini sebagai sesuatu yang luarbiasa.

Kedua orang tuanya, guru matematik di Hongaria, adalah yang pertama kali mendidiknya di rumah. Ia sulit menyesuaikan diri dengan kedisiplinan sekolah. Ia memasuki Universitas Pazmany Peter, Budapest, umur 17 tahun, meraih gelar Doktor umur 21, dan terus belajar ke London. Sejak itu, ia tak pernah berhenti bergerak, tak pernah bisa menetap lebih dari 1 bulan di 1 tempat. “Sangat penting baginya untuk sama sekali bebas,” kata seorang teman. “Ia tak bisa menerima setiap macam ‘paksaan’ yang membatasinya keluarga, rumah, atau jadi dosen. Bahkan sulit baginya untuk tinggal di satu kamar lama-lama.” Tambah Graham, “Dia selalu tahu, pasti ada persoalan baru di tempat lain. Kalau dia sudah mulai berbicara tentang politik, berarti ia merasa bahwa sudah tak ada lagi masalah matematik di tempat itu. Ia sudah siap untuk pergi lagi.”

Kenapa tak kawin? “Rumit, memang,” kata Erdos. “Saya tak pernah tahan kenikmatan seksual. Sifat saya dari kecil adalah selalu ingin berbeda dengan orang lain. Sifat ini sudah mendalam sekali. Dari kecil saya segera menolak setiap tekanan supaya seperti orang lain.”

Besoknya, Erdos sudah pergi lagi ke Universitas McGill, di Calgary, menemui ahli matematik Willy Moser. Moser senang dengan Erdos. Ia sangat menghargai jasa Erdos bagi bergenerasi mahasiswa. “Pasti ada lebih dari 100 matematikawan kini yang mendapat jabatan tetap atau gelar akademik berkat persoalan yang diajukan dan bantu dipecahkan oleh Erdos,” kata Moser.

Sebelas ribu meter di udara, Erdos sedang mengobrol dengan para penumpang pesawat lainnya. Dia sama. sekali tak mengerti kenapa orang senang membeli sesuatu, seperti baju (baju yang dipakainya sudah 4 hari), dan tak bisa membedakan satu makanan dengan makanan lainnya. Bahkan dia pun tak tahu apa itu Walkman *Sony. Seorang penumpang, tergerak oleh pengakuan si kakek ini, meminjamnya sebuah Walkman. Erdos, dengan penuh curiga , memasang ear-phonenya. Wajahnya langsung heran. “Suaranya bagus sekali,” serunya. Dia senang, tentu, karena salah satu yang dinikmatinya selain matematik adalah musik klasik . Cuma, satu-satunya barang lux yang dibawa-bawanya, adalah sebuah transistor kuno bersuara kaleng. Ketika dianjurkan supaya lebih baik membawa Walkman karena lebih praktis, Erdos berkeras. “Saya rasa tidak. Repot juga membawa-bawanya ,” katanya, sambil mengembalikannya ke si pemilik dan kelihatan lega bisa melepaskan satu daya pikat keduniaan lagi. Ia sungguh bingung bila ditanya apakah dia tidak menyesal mengorbankan hal-hal semacam ini dalam hidupnya. “Saya tidak pernah merasa bahwa itu adalah pengorbanan,” katanya. “Saya. tak pernah ingin memiliki sesuatupun. Menurut orang Yunani kuno, orang bijaksana tidak memiliki apapun yang tidak bisa dibawa di tangannya. Kalau anda mempunyai sesuatu yang berharga, anda terpaksa harus menjaganya, jadi saya lebih baik memberinya saja.” Ini bukan cara yang dipilihnya, tambahnya. Juga, ia sama sekali tak pernah memilih matematik sebagai kerjanya setiap hari. “Bagi saya, ini adalah sesuatu yang alamiah seperti bernafas.”

Memang, Berjalan dengan sandal dan jas butut abadinya, kepala menunduk, mata menerawang memandang ubin, otaknya sedang melahap makanan lain: Andaikan n adalah bilangan bulat positif . . . (J. Tiernev)

————————————-
Main-main dengan Angka

Coba saja perhatikan sekeliling anda, pasti ada pola-pola tertentu yang terlalu teratur untuk di-bilang tak disengaja —bebatuan yang begitu tepatnya membentuk formasi geometris, bintang beraturan dalam konstelasi, angka-angka tertentu yang secara misterius selalu timbul berulangkali, dan sebagainya. Manusia, biasanya, karena tak tahu, mencari-cari alasannya yang sering berhubungan dengan kekuatan gaib atau mahluk-mahluk antariksa. Tapi, kelihatannya, lebih baik untuk berpaling ke Paul Erdos dan Frank Ramsey. Teori mereka menunjukkan bagairnana suatu pola tertentu pasti timbul pada suatu kelompok obyek.

Teori Ramsey, sebutan nama cabang matematika ini, dari nama seorang matematikawan brilian Universitas Cambridge, Frank Plumpton Ramsey, Teorinya, rumit memang, tentang rangkaian-rangkalan tak terhingga (infinite sets) yang intinya: “ketidakteraturan sempurna adalah mustahil” Teori ini, tak banyak yang memperhatikannya, sewaktu dikemukakan tahun 1930. Tapi, tak lama kemudian, Erdos dan beberapa teman kuliahnya, melihat bahwa tak perduli bagaimana acaknya mereka menyebarkan titik-titik pada sebuah bidang, ternyata, hasil mereka sama dengan karya Ramsey yang waktu itu belum mereka ketahui. Karena makalah Erdos inilah, diterbitkan tahun 1935, teori Ramsey mulai digandrungi, membuka cabang baru dalam matematika.

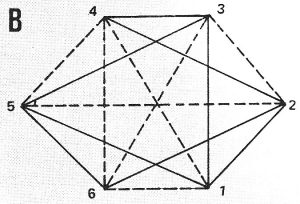Contoh klasik teori Ramsey adalah yang disebut soal “jamuan santap malam”: Cari jumlah minimum tetamu yang menjamin bahwa paling tidak 3 tamu adalah sahabat akrab, atau paling tidak 3 tamu belum saling mengenal. Gambaran matematis ini disebut grafik komplit (complete graph ) —sekumpulan titik yang kesemuanya dihu-bungkan garis. Setiap titik (tamu) dihubungkan ke setiap titik oleh garis merah (di sini dibuat garis ptrtus) yang berarti keduanya saling mengenal, atau oleh garis biru yang berarti mereka tak saling mengenal, Soalnya adalah mencari jumlah titik minimum sehingga, tak perduli warna apa yang anda pilih, selalu harus ada segitiga merah atau segitiga b ru. 5 titik tak cukup, karena anda bisa mewarnai garis sehingga tak ada 3 titik yang membentuk segitiga biru atau merah, seperti gambar 1. Tapi, dengan 6 titik, anda tak dapat menghindar membuat segitiga dalam satu warna. Pada gambar 2, misalnya, segitiga merah menghubungi titik-titik 1, 4, dan 6.

Pilih struktur berukuran apapun, pasti akan terwujud dalam satu warna kalau titik yang anda pilih cocok.

Tentu grafik akan semakin rumit kalau semakin besar. Bisa membuat grafik bertitik 6000 tapi tidak mengandung 20 titik yang terhubung oleh atu warna? Bisa, cuma tak ada manusia maupun komputer yang mampu menggambarnya —jaringan penghubung itu terlalu amat-rumit. Untuk menjawabnya, harus dipakai pendekatan tak langsung, jalan pintas yang dicetuskan Erdos. Dengan cara ini, anda menghitung berapa banyak cara “salah” untuk mewarnai grafik bertitik 6000 sehingga mengandung 20 titik yang terhubung oleh satu warna. Tentu, mustahil untuk menghitung persis jumlah pewarnaan salah ini, tapi anda bisa membuat perkiraannya. Ternyata, jumlah ini lebih rendah daripada jumlah total cara mewarnai grafik bertitik 6000. iadi, pasti ada beberapa cara pewarnaan “benar” yang tidak mengandung 20 titik yang terhubung oleh satu warna.

Pendekatan Erdos ini disebut cara
pernbuktian nonkonstruktif, karena tak memberitahu bagaimana caranya membuat grafik bertitik 6000 seperti diinginkan, tetapi cuma bahwa grafik itu ada. la pun tak memberi jawaban pasti. Karena tentu ada kesalahan dalam proses perkiraan itu, tak ada yang pasti apa grafik terkecil yang harus mengandung 20 titik yang terhubung dengan warna sama. Yang diketahui: ia pasti lebih besar dari 6000 titik dan lebih kecil dari 35 milyar titik.

Ada alasan kenapa harus meruperdulikan grafik semacam ini? Struktur grafik semacam ini, katanya, model baik untuk jaringan-jaringan komunikasi. Dengan mengembangkan cara menghitung sifat sebuah grafik raksasa, Erdos secara tak langsung mungkin membantu insinyur mendisain jaringan-jaringan amat luas yang menghubungkan komputer dan telpon. Namun, Erdos sendiri, tak mau tahu. la mempelajari grafik ini hanya karena menurut dia menarik. Itu saja!

Sumber: Majalah AKU TAHU/Januari 1985