Chaos

Ternyata ada sistem sederhana dengan hanya satu atau dua derajat kebebasan yang memperlihatkan sifat acak seperti yang dimiliki oleh sistem dengan derajat bebas sangat besar.

PADA hekekatnya, ilmu pengetahuan didasarkan pada hubungan yang jelas antara sebab dan akibat sehingga —misalnya— dengan hukum-hukum gravitasi, gerhana matahari dapat diramalkan secara teliti untuk ribuan tahun mendatang. Walaupun demikian, ada fenomena-fenomena alam yang tidak dapat dijabarkan secara pasti (eksak) melainkan mentak (probabilistik). Misalnya, cuaca di bumi tidak bisa dipastikan untuk 24 jam mendatang, apalagi untuk ribuan tahun di muka. Walaupun gerakan-gerakan atmosfer bumi mengikuti hukum-hukum fisika seperti halnya. dengan gerakan planet-planet. Perubahan cuaca, aliran sungai, gerakan molekul-molekul gas semuanya tidak dapat dipastikan dan dikatakag bersifat acak. Tidak ada hubungan yang jelas antara sebab dan akibat dalam fenomena-fenomena tersebut. Meskipun demikian, pendekatan, pendekatan statistik memungkinkan kita meramalkan dan menggambarkan kejadian-kejadian alam itu dengan cukup teliti asalkan syarat-syarat statistikalnya dipenuhi. Seperti yang telah dilakukan orang dalam fisika statistik untuk mempredeksi perilaku sejumlah besar molekul-molekul gas, misalnya dengan merata-ratakan besaran-besaran fisis dari tiap molekul gas tersebut.

Tapi sebuah penemuan baru merombak padangan di atas. Ternyata ada sistem sederhana dengan hanya satu atau dua derajat kebebasan yang memperlihatkan sifat acak seperti yang dimiliki oleh sistem dengan derajat bebas sangat besar. Yang mengherankan adalah bahwa sifat acak itu berasal dari hukum-hukum fisika yang pasti (eksak/deterministik), seperti hukum Newton II. dan sama sekali tidak mengandung faktor kementakan. Sistem itu dikatakan dalam keadaan CHAOS.

Hukum Newton II menyatakan jika gaya F bekerja pada sebuah benda ber-massa m, maka benda tersebut memiliki percepatan a. Misalkan kita juga mengetahui posisi dan kecepatan benda ter-sebut pada suatu waktu (s dan v pada t=t0), dengan kalkulus dasar posisi dan kecepatan benda itu dapat ditentukan selamanya. Artinya, dengan berbekal informasi keadaan sistem pada suatu waktu dan aturan yang menyatakan bagaimana sistem itu berubah menurut waktu, kita dapat menentukan perilaku sistem itu selamanya. Atas dasar inilah matematikawan Prancis, Pierre Simon de Laplace, pada abad ke-18, pernah sesumbar jika diberitahukan kepadanya posisi dan kecepatan dari setiap partikel di alam semesta. Laplace dapat meramalkan masa depan alam semesta ini! Walaupun ada banyak kesulitan untuk mempraktekannya, pendapat Laplace ini pada prinsipnya dapat diterima dan telah dianut banyak orang selama lebih dari seratus tahun.

Pada abad 20, pendapat Laplace tersebut gugur karena dua hal. Pertama, prinsip ketidakpastian Heisenberg menyatakan tidak mungkin kita mengetahui keadaan suatu sistem dengan tepat. Posisi dan kecepatan dari sebuah partikel tidak dapat diketahui sekaligus dengan ketelitian 100 persen. Prinsip ini dapat menjelaskan beberapa peristiwa yang bersifat acak seperti peluruhan inti. Inti yang begitu kecil mengakibatkan efek ketidakpastian Heisenberg tak terabaikan. Ada batas tertentu untuk mengetahui gerakannya sehingga kita tidak tahu kapan tepatnya inti itu mulai meluruh.

KETIDAKPASTIAN
Lalu apakah ketidakpastian dalam skala mikroskopis ini yang menyebab-kan perilaku acak beberapa sistem-sistem makroskopis?

Henry Poincare, matematikawan abad 20 dari Prancis, menyatakan bahwa pada sistem tertentu perubahan kecil pada masa sekarang membuat perbedaan yang besar pada masa mendatang. Seperti sebuah batu karang yang ada di puncak bukit, sentuhan ringan dalam arah yang berbeda menyababkan batu itu menggelinding ke bawah dengan lintasan yang jauh berbeda. Contoh lain yang menggambarkan betapa pekanya beberapa sistem fisika terhadap pengaruh kecil dari luar adalah pada permainan bola sodok. Kita ambil keadaan idealnya saja yakni setiap tumbukan adalah lenting sempurna dan tidak ada gesekan. Dengan sekali sodok seorang pemain membuat bola-bola sodok saling bertumbukan dan menyebar terus menerus. Ia tentu ingin mengetahui akibat dari sodokannya.

Sampai berapa jauh seorang pemain dengan kontrol sodokan yang sangat baik dapat meramalkan lintasan dari bola gacoannya? Bahkan kesalahan kecil sebesar gaya gravitasi elektron di ujung galaksipun mampu membuat prakiraan si pemain. menjadi salah dalam satu menit.

Perkembangan ketidaktelitian awal yang cepat ini disebabkan karena bola-bola itu bulat dan perbedaan titik tumbuk bola dengan bola diperkuat pada setiap tumbukan berikutnya. Pertumbuhan ketidakpastian ini bersifat eksponensial, selalu bertambah besar pada setiap tumbukan. Setiap efek berskala mikroskopis dengan cepat membengkak menjadi efek makroskopis. Inilah salah satu ciri keadaan CHAOS.

Jadi faktor kedua yang menggugurkan pendapat Laplace di atas adalah pertumbuhan eksponensial ketidakpastian awal itu (ketidakpastian Heisenberg) dalam keadaan CHAOS. Mekanika kuantum menjamin bahwa selalu ada ketidakpastian dalam pengukuran keadaan awal dan dinamika CHAOS menjadi ketidakpastian tersebut membengkak dengan cepat sehingga kita tidak dapat membuat perkiraan apapun. Tanpa CHAOS Laplace mungkin berharap kesalahan awal itu tetap terbatas atau minimal bertambah besar dengan lambat sehingga ia masih bisa membuat perkiraan untuk waktu yang cukup lama. Dengan adanya CHAOS ramalannya itu dengan segera menjadi salah.

Sampai di sini kita telah mendapatkan gambaran intuitif tentang CHAOS. CHAOS adalah istilah teknis untuk menggambarkan keadaan tak teratur, perilaku acak dari sis-tem yang nonlinear namun determninistik.

Sekarang akan diperlihatkan dua contoh sistem dalam keadaan CHAOS — sistem yang berperilaku acak kendati hukum fisika yang mengaturnya bersifat pasti (eksak/determinasi).

Contoh 1: Bayangkan sebuah rangkaian tiga amplifier. Amplifier I mengeluarkan sebuah sinyal x yang diumpan ke amplifier II dan III. Sebagai respons, amplifier II ini mengeluarkan sinyal (1-x) yang diumpan ke amplifier III. Amplifier III, yang menerima input dari Amplifier I dan II, mengalikan input ini dan mengeluarkan hasilnya x(x-1) yang diumpan balik ke Amplifier I. Amplifier III juga menerima tegangan pada amplifier I. Rangkaian ini ternyata memperlihatkan tariantegangan yang makin seru seiring dengan naiknya tegangan kontrol, r.

Ketika harga r 3, tegangan berisolasi sebentar dan dengan cepat mencapai titik seimbangnya pada harga tertentu untuk selamanya. Ini adalah contoh penarik (atractor) tunggal. Tapi begitu r sedikit di atas 3, rangkaian ini berisolasi pada dua nilai tegangan—keadaan bistabil (dua titik penarik). Jika r dinaikkan terus, rangkaian akan berisolasi pada 4 titik, 8 titik, dan seterusnya. Pada r kira-kira 3,5,tarian tiba-tiba menjadi tak karuan, tegangan berubah-ubah tinggi – rendah, tak menentu terus menerus. Titik penariknya menjadi banyak tak berhingga. Keadaan ini disebut CHAOS.

Kita dapat mensimulasi rangkaian di atas, pada komputer, dengan program yang intinya:

input r
x <— 3
for i <—- 1 to 200
x <—- rx (1-x)
for i <—- 1 to 300
x <—- rx (1-x)
plot (200x,100r)

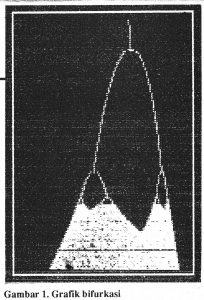
Mula-mula kita berikan harga untuk x samadengan 0,3. Lalu 200 iterasi pertama adalah untuk menghilangkan efek transien pada persamaan ini sampai diperoleh nilai x yang stabil. Kemudian dalam 300 iterasi berikutnya, nilai x di plot. Grafik r versus x ini dinamakan diagram bifurkasi. Seperti penjelasan di atas, untuk r 3,5 diagram ini mencerminkan sistem dinamis sederhana dengan beberapa titik seimbang, tapi untuk r 3,5 (tepatnya 3,56994571869) keteraturan ini terhenti. Keadaan kacau balau atau CHAOS. Peristiwa itu sendiri eksak dalam arti tak ada alternatif lain dari ‘jalan’ yang harus ditempuh. Masa depannya sepenuhnya tergantung pada kondisi awal x = 0,3. Pernilihan kondisi awal yang lain, bahkan yang hampir sama sekalipun, akan meng-akibatkan nilai-nilai x berikutnya jauh berbeda.

2. Sebuah rotor ditendang horisontal secara periodik. Misalkan x adalah sudut rotor pada saat tendangan ke-n, y adalah kecepatan angular rotor segera sesudah tendangan ke-n. Sesuai hukum Newton II, dalam satu selang waktu:

yn+i = yn + k sin (xn) (1)
Yn+1 Xn + Yn+1 (2)

k : parameter yang menentukan tendangan maksimum. Kedua persamaan ini adalah aturan yang menjelaskan bagaimana keadaan sistem ini (x,y) berubah dari waktu ke waktu. Perubahannya sendiri bisa kita lihat dalam ‘ruang keadaan’ (lihat box “Kisah Sebuah Bandul”) untuk sistem dinamis ini.

Dengan komputer, persamaan iterasi (1) dan (2) ini dikerjakan untuk berbagai nilai kondisi awal (x,y). Suatu keuntungan yang menyederhanakan persoalan adalah bahwa harga x dan y periodik yang menyederhanakan persoalan adalah bahwa harga x dan y periodik setiap 2?. Diagram alir persoalan di atas:
input x,y,n,k
for i 1 to n
y <— (y + k sin (x)) mod 2?
x <—-(x + y) mod 2?
plot (x,y)

Tanpa hadirnya penarik (atractor), titik fase ruang keadaan (x,y) pada prinsipnya dapat mengembara kemana saja di ruang keadaan. Tapi untuk k = 0 (berarti rotor tidak ditendang) terjadi perubahan keadaan sistem yang teratur. Rotor berputar dengan kecepatan konstan yakni y, diwakili oleh garis lurus sejajar sumbu x di ruang keadaan x-y. Energi kinetik rotor dengan demikian konstan. Untuk nilai k yang kecil, bentuk petanya masih teratur, artinya perubahan keadaan sis-tem masih dapat diramalkan. Energi dan kecepatan yang dimiliki rotor terbatas pada daerah tertentu sepanjang waktu. Tapi untuk harga k yang lebih besar (k0,971635406), bentuk petanya menjadi tak teratur (meski ada bagian peta yang teratur). Kecepatan dan energi rotor ‘bebas mengembara’ ke mana saja di ruang keadaan. Kecepatan dan energi rotor ini seolah berjalan acak, walaupun kelakuannya ini ditentukan oleh persamaan (1) dan (2) di atas. Itulah CAHOS!!!!
————————————–
KISAH SEBUAH BANDUL

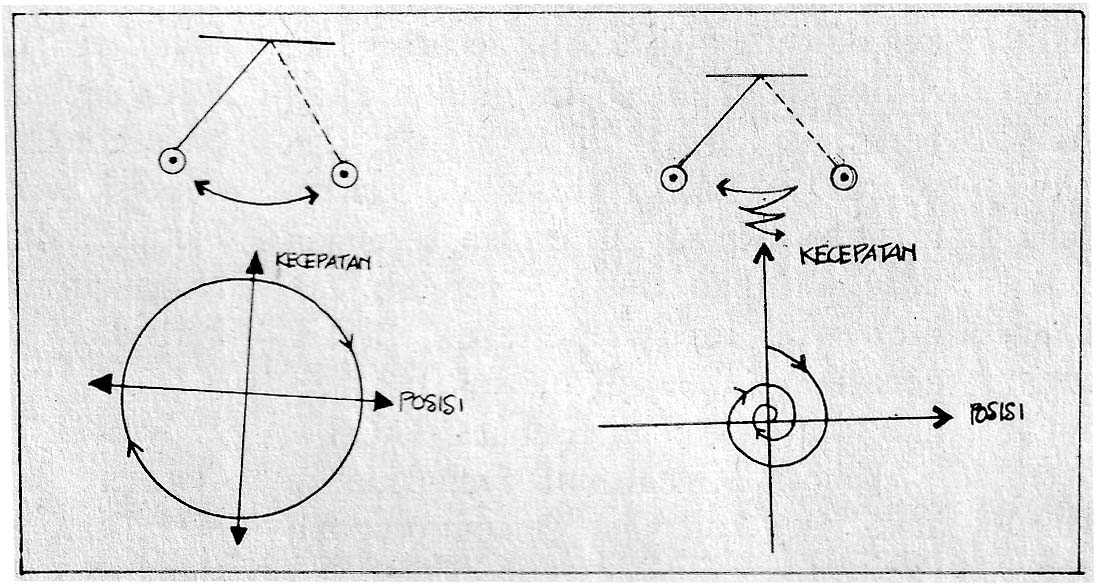
SEBUAH sistem dinamis terdiri atas dua bagian: sebuah pemyataan keadaan sistem pada waktu tertentu dan aturan yang menjelaskan perubahan keadaan sistem dari waktu ke waktu. Perubahan ini dapat divisualisasikan ke dalam suatu ruang abstrak bernama ‘ruang keadaan’. Koordinat ‘ruang keadaan’ ini adalah komponen keadaan sistem. Untuk sistem mekanika, koordinat yang dipakai biasanya posisi dan kecepatan dari anggota sistem.

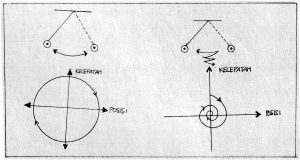
Kita ambil contoh ayunan sederhana. Komponen keadaan sistem ini adalah posisi (x) dan kecepatan (v) bandul. Keadaan sistem pada waktu t diwakili oleh satu titik (x,y) pada ruang keadaan. Hukum Newton II menjelaskan perubahan keadaan sistem dari waktu ke waktu, tertuang dalam sebuah persamaan diferensial. Dalam keadaan ideal sistem ‘bergerak’ dalam ruang keadaan membentuk orbit tertutup berbentuk lingkaran (gambar 1). Kehadiran gaya gesek menyebabkan orbit berbentuk spiral yang mengecil, menuju titik keseimbangan (Gambar 2)

Titik ini dalam ruang keadaan disebut ‘penarik’ (atractor) karena titik ini seolah menarik orbit-orbit di dekatnya. Jika bandul diberi gangguan lagi, maka suatu waktu bandul akan kembali diam di titik yang sama. Beberapa sistem memiliki lebih dari satu titik penarik atau sebuah garis penarik bahkan kurva penarik. Untuk keadaan CHAOS, penariknya berbentuk permukaan tak rata tapi terlipat-lipat.

Oleh. Joshua Arif Tanja

Sumber: Majalah AKUTAHU/JULI 1990