Konstanta Pi

Dengan bantuan komputer, pi sampai 500.000 letak desimal pun telah dihitung orang. Apa gunanya ?

Murid sekarang cukup beruntung. Dengan hanya menyebutkan pi (?) kali diameter, mereka sudah dapat menyatakan keliling lingkaran. Tidak demikian halnya bagi orang yang hidup di abad pertengahan. Di dalam bahasa Latin, untuk pi saja, mereka harus menyebut quantitas, in quam cum multiplicetur diameter, proveniet circumferentia. Artinya: kuantitas yang, jika diameter dikalikan dengannya, memberikan keliling.

Pada zaman itu, penyebutan luas lingkaran adalah lebih rumit lagi: Multiplicatio medietatis diametri in se ejus,quod proveniet, in quantitatem, in quam cum multiplicatus diameter provenit circumgerentia, aequalis superficies circuli. Artinya: pengalian separuh diameter dengan dirinya sendiri dan dengan yang dihasilkan oleh kuantitas yang, jika diameter dikalikan dengannya, menghasilkan keliling, sama dengan Iuas lingkaran.

Kini, betapa leganya kita yang hidup pada zaman ini, karena kita sudah memiliki nama konstanta pi untuk menyatakan keliling dan luas lingkaran. Keliling lingkaran adalah pi kali diameter sedangkan luas lingkaran adalah pi kali jari-jari kuadrat. Cukup sederhana!

Persoalannya, kini, berapa nilai konstanta pi itu? Di sekolah dasar, guru mengatakan bahwa nilai pi adalah 22/7 Di sekolah yang lebih tinggi, guru mengatakan bahwa pi adalah 3,1416. Dan di kalangan penggemar pi, nilai itu di cari sampai ke banyak letak desimal. Sampai tahun 1967, dengan bantuan komputer, sudah ada orang yang menghitung nilai pi sampai 500.000 letak pecahan desimal.

Bermacam Nilai Pi. Sudah sejak zaman kuno, manusia menyadari bahwa keliling serta luas lingkaran bergantung kepada diameter lingkaran itu. Makin besar diameternya, makin besar pula keliling dan luas lingkaran. Bahkan, mereka telah menemukan bahwa ada suatu konstanta yang menghubungkan keliling dan diameter lingkaran. Secara tidak langsung, Kitab Injil Perjanjian Lama memuat ungkapan tentang pi ini, Pada I Raja-raja 7:23, tercatat:

Kemudian dibuatnyalah “laut” tuangan yang sepuluh hasta dari tepi ke tepi, bundar keliling, lima hasta tingginya, dan yang dapat dililit berkeliling oleh tali Yang tiga puluh hasta panjangnya.

Coba saja kita hitung. Sepuluh hasta dari tepi ke tepi dengan keliling 30 hasta akan menghasilkan nilai pi sebesar 3.

Kita mengetahui bahwa nilai pi lebih dari 3. Dalam hal ini, pada tahun 150, seorang rabi dari Iberani yang menjadi ahli ilmu ukur menyatakan bahwa nilai pi adalah 3 1/7 Di dalam bukunya, yang berjudul Mishnat ha-Middot, Rabi Nehemiah berkata bahwa 1/7 itu adalah tebal “laut” tuangan itu. Entahlah, sampai di mana kekuatan argumentasi sang rabi. Tetapi, pada beberapa ayat kemudian, yakni 7:26, tercatat:

Tebal “laut” itu setapak tangan dan tepinya serupa tepi piala, seperti bunga bakung yang berkembang. “Laut” itu dapat memuat dua ribu bat air.

Lepas dari Kitab Injil ini, nilai pi sudah sejak lama dibahas orang di berbagai pusat kebudayaan. Nilainya pun berbeda-beda. Namun, cara untuk menghitungnya adalah bersamaan. Mereka membuat segi beraturan di luar dan di dalam lingkaran. Ukuran keliling dan luas segi beraturan mudah dihitung sehingga ukuran keliling dan luas lingkaran pasti terletak di antara kedua segi beraturan itu.

Pada tahun 1936, para ilmuwan menemukan suatu bata bertulis zaman kuno yang terletak sekitar 300 km dari Babylon. Pada bata bertulis itu tercantum:

perimeter segienam beraturan                 57    36
—————————————— = — + —
keliling lingkaran                                      60    3600

Pembagian 60 dan 3600 itu muncul dari cara mereka berhitung yang menggunakan sistem bilangan seksagesimal (enampuluh). Kalau rumusan ini kita hitung, maka akan kita temukan bahwa pi = 3,125 atau pi = 3 1/8.

Dari zaman Mesir Kuno, terdapat suatu papyrus yang dikenal sebagai Papyrus Ahmes yang berisikan matematika. Pada tulisan nomor 50, tercatat rumusan yang menjurus ke penentuan nilai pi. Dinyatakan bahwa luas lingkaran dengan diameter 9 satuan adalah sama dengan luas bujur sangkar yang bersisi 8 satuan. Dari pernyataan ini, kita temukan bahwa:

pi = 4 x (8/9) x (8/9)
= 3,16049…

Pernyataan ini menunjukkan satu hal yang penting. Di situ, orang Mesir Kuno sudah mengemukakan gagasan tentang pembujursangkaran lingkaran. Pembujursangkaran lingkaran atau mengubah lingkaran menjadi bujur sangkar yang sama luasnya, kemudian menjadi suatu soal yang menarik perhatian kalangan ahli matematika di Yunani Kuno.

Dari catatan yang kita ketahui sekarang ini, nilai pi dari Mesopotamia dan dari Mesir Kuno adalah catatan terkuno yang pernah kita miliki. Kedua kebudayaan ini menggunakan sistem bilangan yang berbeda. Mesopotamia menggunakan dasar bilangan seksagesimal dan, walaupun tidak sempurna, sudah menggunakan sistem letak. Sebaliknya, Mesir Kuno menggunakan dasar bilangan desimal, namun mereka tidak menggunakan sistem letak. Dari rumusan di atas tampak bahwa sistem bilangan ini berpengaruh juga terhadap ketelitian penentuan nilai pi.

Jauh setelah zaman Mesopotamia dan Mesir Kuno, di Cina Kuno terdapat catatan tentang nilai pi. Sudah sejak awal, Cina Kuno menggunakan dasar bilangan desimal dan sistem letak, seperti yang kita kenal sekarang. Sekalipun demikian, cukup lama pula mereka menggunakan pi yang bernilai 3. Barulah kemudian, pada tahun 130, Hou Han Shu mengguriakan pi yang bernilai 3,1622.

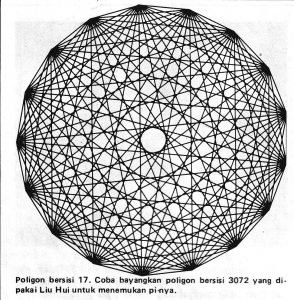
Pada tahun 264, Liu Hui menggunakan poligon luar dan poligon dalam lingkaran untuk menentukan nilai pi. Dengan poligon bersisi 192, Liu Hui menemukan nilai pi,

3,141024 < pi < 3,142704

dan dengan poligon bersisi 3072, Liu Hui menemukan bahwa pi bernilai 3,14159.

Pada abad kelima, Tsu Chung-Chih bersama anaknya Tsu Keng-Chih menemukan nilai pi di antara 3,1415926 < pi < 3,1415927

Anehnya, pada tahun 718, terdapat naskah yang mengambil nilai pi sebesar 92/29 yakni 3,1724 . . . yang kalah teliti dari nilai yang digunakan pada beberapa abad sebelumnya.

Di India Lama, salah satu buku Siddhanta yang terbit pada tahun 380, mencatat nilai pi,

pi = 3 177/1250
= 3,1416

Pada tahun 499, di dalam bukunya Aryabhatiya, Aryabhata mengemukakan nilai pi melalui suatu uraian sebagai berikut:

Tambahkan 4 ke 100, kalikan dengan 8, dan tambahkan 62.000. Hasilnya adalah kira-kira sama dengan keliling lingkaran yang diametemya 20.000.

Kalau rumusan ini kita hitung, maka kita peroleh nilai pi sebesar 3,1416.

Pada abad ke-12, Bashkara menemukan nilai yang sama. Namun, berbeda dengan Aryabhata, Bashkara menganggap bahwa nilai ini adalah “tepat.”

Pada abad ke-7, Brahmagupta menganggap bahwa nilai pi sama dengan akardua dari 10. Dalam bentuk pencahan desimal, nilai Brahmagupta ini menjadi 3,162277…

Ahli Yunani Kuno menemukan metoda yang cukup ampuh. Ada asas pengambilan sampai habis dari Antiphon serta ada reductio ad absurdum dari Hippocrates dari Chios. Dengan metoda yang mereka temukan, orang Yunani Kuno, seperti Anaxagoras dari Clazomenae, mencoba untuk membujursangkarkan lingkaran. Hal ini kemudian menarik banyak perhatian ahli matematika Yunani Kuno. Namun, di samping metoda, mereka juga menghitung nilai pi. Salah satu nilai yang mereka gunakan adalah

pi = 3 + 8/60 + 30/3600

Dengan menggunakan metoda poligon, Archimedes menemukan, melalui poligon bersisi 96, bahwa nilai pi terletak di antara

3 10/71 < pi < 3 1/7

atau dalam bentuk pecahan desimal, di antara

3,140845 … < pi < 3,142857 …

Di dalam bukunya yang berjudul Metrica, Heron dari Alexandria mengemukakan rumusan Archimedes,

211875 : 67441 < pi < u

dengan u sebagai batas atas nilai pi. Dalam hal ini, Heron mengemukakan bahwa batas atas itu adalah

u = 197888 : 62351
= 3,1738

Sekalipun demikian, Heron menambahkan pula, “Karena bilangan ini tidak memudahkan untuk pengukuran, maka mereka disederhanakan ke perbandingan bilangan yang lebih kecil, yakni 22:7.” Angka ini pula yang kemudian sampai ke sekolah dasiar kita di sini.

Sementara itu, Ptolemy dari Mexandria, menggunakan pi yang bernilai,

pi = 377/120 atau 3 17/120

Pada zaman kemudian, yakni abad ke-13, Fibonacci menggunakan pi yang bemilai,

pi = 864 : 275
= 3,141818

Gerbert atau Paus Silvester menggunakan nilai pi = 22/7. Kecuali Albert von Sachen pada abad ke-12 yang mengatakan bahwa “mengikuti pernyataan banyak ahli filsafat,

pi = tepat 22/7

ada bukti, tetapi sulit,” maka para ahli matematika kemudian mengetahui bagaimana caranya mencari nilai pi yang setepat mungkin. Bahkan, Francois Viete, mengemukakan rumusan pi yang rumit, terdiri atas banyak akardua dari 1/2. Rumusan itu terlalu rumit untuk ditulis di sini.

Para ahli itu kemudian mengetahui bahwa nilai pi adalah irasional, yakni tidak mungkin ditulis dalam bentuk pecahan dengan pembilang dan penyebut. Dan kalau ditulis dalam bentuk pecahan desimal, maka letak pecahan desimal itu tidak akan berkesudahan.

Lomba Banyak Digit. Pengetahuan akan keirasionalan nilai pi membawa ahli matematika ke arah pencarian digit pecahan desimal. Bahkan terjadi perlombaan tak resmi di antara mereka untuk menemukan lebih banyak digit lagi.

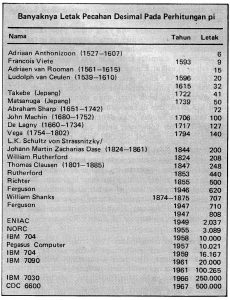
Coba kita lihat. Adriaan Anthonizoon (1527-1607) menghitung sampai 6 ,letak desimal. Pada tahun 1593, Francois Viete menghitung sampai 9 letak desimal. Adriaen van Rooman (1561-1615) menghitung sampai 15 letak desimal. Ludolph van Ceulen (1539-1610), pada tahun 1596, menghitung sampai 20 letak desimal, dan kemudian, pada tahun 1615, isterinya mengumumkan perhitungan van Ceulen sampai 32 letak desimal. Pada tahun 1722, Takebe menghitung sampai 41 letak desimal. Masih banyak lagi, sehingga lebih baik kita susun saja perhitungan itu dalam bentuk tabel.

Tampak dari tabel itu bahwa sampai pada tahun 1967, dengan bantuan komputer, sudah ada orang yang menghitung pi sampai 500.000 letak desimal. Dua ratus di antara 100265 letak desimal yang dihitung pada tahun 1961, ditampilkan pada tulisan ini.

Demikian banyaknya letak desimal pada nilai pi tentunya tidak lagi mempunyai kegunaan praktis. Selain untuk sekedar keingintahuan, demikian banyak letak desimal untuk nilai pi dapat digunakan untuk studi. Ada saja para ahli yang ingin menyelidiki susunan angka di dalam nilai pi itu. Barangkali pula ada di antaranya yang cukup menarik perhatian. Coba saja perhatikan. Apa yang dapat kita temukan pada deretan dua ratus letak desimal dari nilai pi itu?

Dua ratus di antara 100.265 letak desimal yang dihitung pada tahun 1961.

PI = 3…
1415926535 8979323646 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 44211810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4862046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 6602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344161 5981362977 4771309960 5187072113 4999999837 2976049951 ‘0597317328 1609631859 5024459455 3469083026 4252230825 33446B5035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 164201989

3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959 5082953311 6861727855 8890750983 8175463746 4939319255 0604009277 0167113900 9846824012 8583616[135 6370766010 4710181942 9555961989 4676783744 9448255379 7747268471 0404753464 6208046684 2590694912 9331367702 8989152104 7521620569 6602405803 8150193511 2533824300 3558764024 7496473263 9141992726 0426992279 6782354781 6360093417 2164121992 4586315030 2861829745 5570674983 8505494588 5869269956 9092721079 7509302955 3211653449 8720275596 0236480665 4991198818 3479775356 6369807426 5425278625 5181841757 4672890977 7727938000 8164706001 6145249192 1732172147 7235014144 1973568548 1613611573 5255213347 5741849468 4385233239 0739414333 4547762416 8625189835 6948556209 9219222184 2725502542 5688767179 0494601653 4668049886 2723279176 6085784383 8279679766 8145410095 3883786360 9506800642 2512520511 7392984896 0641284886 2694560424 1965285022 2106611863 0674427862 2039194945 0471237137 8696095636 4371917287 4677646575 7396241389 0865832645 9958133904 7802759009

Oleh Dali S. Naga –

AKU TAHU/September 1984

Sumber: AKU TAHU/September 1984