Maksud tulisan ini adalah mencoba menambah informasi pada tulisan bertopik khaos yang disiarkan Harian Kompas, 12 Fabruari lalu: Khaos Akhir Kepastian Sains.
Pada mulanya adalah beberapa gejala alam yang terbukti bertingkah laku rumit, tak teratur tak dapat diprakirakan, dan acak. Gejala alam itu antara lain dijumpai pada aliran turbulen laut, perubahan cuaca, dan pembentukan awan. Kemudian terbukti pula kerumitan dan ketakteraturan dijumpai pada dinamika atoma-atom dan molekul-molekul.
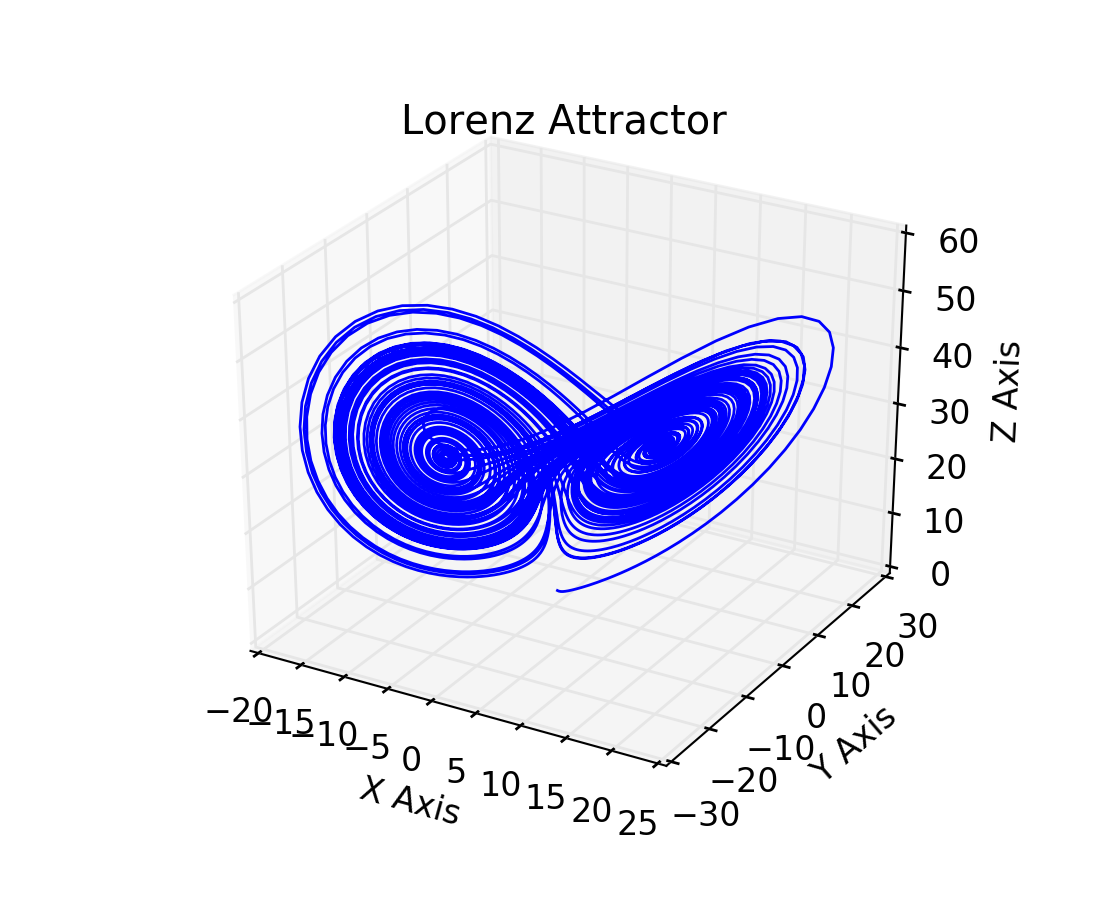
Pada peramalan cuaca, sistem deterministik sederhana , dengan tiga parameter –suhu, tekanan, dan laju angin– ternyata, membuat peramalan jangka panjang menjadi tak karu-karuan. Meteorolog Amerika Serikat; Edward Lorenz, menemukan khaos pada peramalan cuaca di tahun 1963 hanya karena ia membuat pembulatan data numerik ketiga parameter dari enam desimal ke tiga desigmal! Hubungan ketiga parameter yang semula deterministik akhirnya menjadi acak di masa kemudian.
ADVERTISEMENT
SCROLL TO RESUME CONTENT
Pada gerak atom, muncul paradoks. Gerak partikel per individu sifatnya deterministik dan reversibel tapi pada banyak partikel, sifat gerak menjadi acak dan tak reversible. Timbullah satu pertanyaan yang mengganggu. Bagaimana bisa terjadi gerak partikel individual yang masing-masing deterministik dan reversibel malah menyumbangkan tingkah laku sistem tak reversibel pada partikel banyak?
Keacakan ini mendasar. Ia tak hilang sekalipun informasi tentang suatu sistem bertambah Keacakan yang dihasilkan dengan cara seperti itulah yang kemudian disebut chaos atau “galau”.
Deskripsi teoretis tak mampu menguak gejala rumit ini.
Pada turbulensi fluida, biang ketakmampuan itu adalah tak liniernya Persamaan NavierStokes. Pada gerak banyak partikel, kunci kebuntuan memahami kerumitan itu adalah pada format Persamaan Newton untuk banyak partikel.
Keteraturan dalam khaos
Meskipun begitu, pada tahun-tahun terakhir ini banyak kemajuan yang dicapai untuk memahami khaos. Titik terang pemahaman itu didapat dari kombinasi simulasi numerik dan dan pendekatan analitis dengan bantuan komputer digital berkecepatan tinggi.
Grafik komputer dengan resolusi tinggi; memungkinkan para ahli matematika-terapan mengenal dan menyelidiki pola yang muncul dari keluaran (output) komputer. Pakar matematika akhirnya menemukan “keteraturan dalam khaos”.
Dengan itu, lahirlah sebuah paradoks tentang khaos: khaos ternyata deterministik. Masa depan masih dapat ditentukan oleh masa lalu dan masa kini. Hanya saja, ketakpastian atau toleransi yang kecil pada masa kini dapat teramplifikasi sehingga tingkah laku untuk jangka pendek teramalkan, tapi tidak untuk jangka panjang.
Penemuan khaos juga menghasilkan paradigma baru dalam permodelan sains. Di satu sisi paradigma ini mengimplikasikan batas fundamental baru untuk melakukan prakiraan, yakni kemampuan meramalkan terbatas hanya untuk masa depan yang relatif takjauh dari masa kini. Di sisi lain, determinisme pada khaos mengimplikasikan bahwa banyak gejala acak yang ternyata lebih dapat diprakirakan. Khaos memungkinkan ditemukannya keteraturan dalam sistem-sistem yang tampaknya kacau-balau. Khasiat ini telah mengimbas pada banyak disiplin ilmu pengetahuan.
Dinamika tak linier
Pendekatan yang memadukan eksperimen numerik dengan analisis matematika telah melahirkan bidang antardisiplin yang baru: dinamika tak linier. Bidang ini mencakup berbagai problem tak linier pada reaksi kimia, kontrol umpan balik rangkaian listrik, interaksi populasi biologis, respon sel jantung terhadap impuls listrik, naik turunnya harga, dan pembangunan mesin perang dua negara yang bermusuhan.
Para ahli dinamika tak linier menggunakan istilah ”khaos” untuk tingkah laku tak teratur dan tak teramalkan pada sistem deterministik tak linier. Tidak seperti yang dipercaya Isaac Newton, persamaan mekanika klasik yang deterministik ternyata tidak membuktikan alam semesta yang teratur. Bahkan diketahui, hanya sistem-sistem sederhana dengan satu atau dua derajat kebebasan saja yang dapat bersifat khaos.
Sebelum khaos mengamuk di kancah sains pada dasawarsa delapan puluhan, determinisme Laplace sebetulnya sudah terlebih dulu diluluhlantakkan oleh dogma utama mekanika kuantum prinsip ketakpastian Heisenberg.
Berkumandang pada dasawarsa tiga puluhan, dogma ini menyatakan ada batas fundamental pengukuran posisi dan kecepatan partikel. Artinya, posisi dan kecepatan partikel tidak dapat dipastikan secara bersamaan. Manakala kecepatan partikel dapat diketahui pasti, maka kedudukan partikel menjadi sama sekali tak jelas. Prinsip ketakpastian dengan baik dapat menjelaskan peluruhan radioaktif: tidak lagi mungkin mendapatkan informasi yang cukup untuk mengetahui kapan inti (nuklir) suatu atom akan meluruh. Soalnya menjadi probabilistik.
Atraktor
Napas khaos dan statistik probabilitas pada ilmu-ilmu eksak –tentunya sebutan ilmu eksak sekarang perlu diberi persepsi baru — jauh sebelumnya sudah dirasakan matematikawan Perancis Henri Poincare yang hidup di abad lalu. Poincare menyatakan, gejala tak teramalkan terjadi pada sistem yang perubahan kecil saat ini dapat mengakibatkan perubahan besar di masa datang.
Ruamg keadaan sebuah konsep fisika matematika, merupakan sarana yang ampuh untuk menggambarkan perilaku sistem yang bersifat khaos dengan bentuk-bentuk geometri. Ambil contoh gerak bandul yang berangsur-angsur berhenti karena adanya gesekan.
Dengan konsep ruang keadaan dapat dijelaskan, gerak yang perlahan menuju berhenti terjadi karena orbit gerak ini mendekati sebuah titik. Titik yang didekati itu tidak bergerak(tetap), karena itu ia menarik orbit-orbit yang berdekatan dengannya. Titik ini disebut penarik atau atraktor. Setiap sistem yang akhirnya diam dapat dicirikan oleh sebuah titik tetap pada ruang keadaan.
Beberapa sistem tidak berhenti untukjangka waktu yang lama. Sistem demikian sebetulnya mengarungi siklus-siklus yang secara berkala melewati sederetan keadaan. Siklus ini pada waktunya akan mendekati suatu limit: sang penarik. Contoh sistem penarik bersiklus terbatas yang sangat dikenal adalah denyut jantung.
Lalu, jika suatu sistem bersifat khaos, seberapa khaoskah sistem itu? Kekhaosan suatu sistem diukur dengan ”entropi” geraknya dan dimensi sang penarik.
Metode sains
Eksistensi khaos kini mempengaruhi metode sains. Pendekatan klasik untuk membuktikan sebuah teori adalah dengan membuat prakiraan dan mengujinya kemudian dengan fakta empiris. Jika gejalanya bersifat khaos prakiraan jangka panjang menjadi tak mungkin. Ini harus diperhitungkan dalam menilai validitas teori. Maka proses pembuktian teori kini lebih didasarkan pada sifat-sifat statistik dan bentuk geometrinya daripada lewat prakiraan detilnya.
Khaos melontarkan tantangan baru bagi pandangan para reduksionis yang menyatakan, sistem dapat dipahami dengan membagi-bagi sistem itu untuk kemudian setiap bagian dipelajari. Khaos menunjukkan sebuah sistem dapat memiliki perilaku kompleks yang muncul sebagai konsekuensi interaksi sederhana dan tak linier yang terdiri dari beberapa komponen saja.
Khaos acap kali dilihat dalam bentuk pembatasan yang diimplikasikannya, seperti ketidakmampuan melakukan prakiraan. Alam barangkali menggunakan khaos secara konstruktif. Evolusi biologis mengembangkan jenis genetika: khaos memungkinkan penggunaan penstrukturan parubahan acak sehingga penjenisan yang berada di bawah kontrol evolusi dimungkinkan.
Lalu, apa sebenarnya yang kita maksudkan dengan perilaku acak? Intuisi kita tentang proses acak atau peluang, seperti pelemparan dadu, merupakan proses yang menyiratkan perilaku tak teratur yang tidak ditentukan hukum tertentu. Karena itu, definisi tradisional keacakan atau proses stokastik direformulasikan menjadi sebuah sistem dinamis yang dapat diterangkan hanya dengan sifat rata-rata yang ditentukan oleh distribusi probabilitas yang tepat.
Usaha pemaduan hukum-hukum probabilitas mekanika statistik dengan hukum-hukum deterministik mekanika klasik melahirkan cabang baru matematika yang dinamakan teori ergodik. Teori ergodik memungkinkan pengklasifikasian system-sistem dinamis deterministik dengan perilaku tak teratur yang berbeda.
Salah satu sifat yang paling mengejutkan dari sistem dinamis khaos adalah model deterministiknya yang bersifat sederhana. Realisasi perilaku kompleks yang tak membutuhkan model matematika kompleks merupakan sumbangan dinamika tak linier yang paling penting. Karena model-model yang sederhana dapat menghasilkan perilaku yang kompleks dan tidak teratur, maka, kita dapat mengharapkan penggambaran teoritis sejumlah besar gejala alam yang acak dan tak dapat diprakirakan dengan menggunakan model matematika yang menunjukkan perilaku khaos deterministik.***
(Sandi Setiawan, sarjana fisika tinggal di Surabaya)
Sumber: KOMPAS, MINGGU, 21 FEBRUARI 1993
