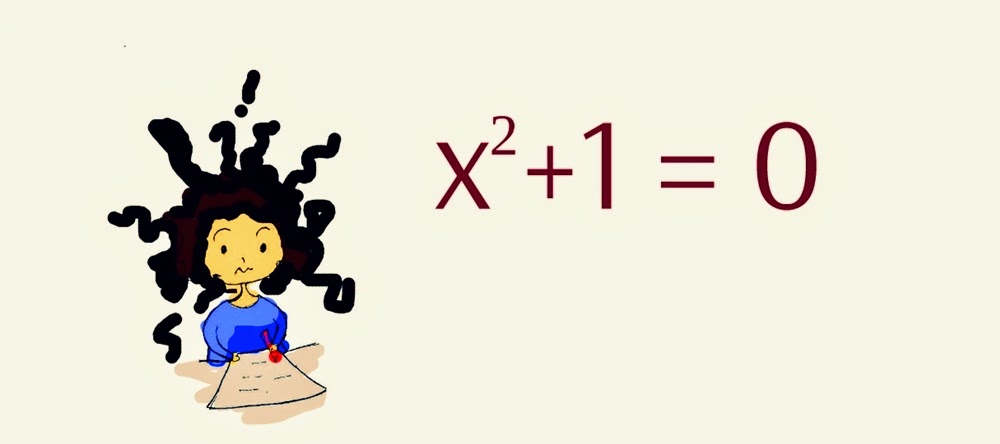Dalam teori bilangan, tentunya anda mengenal adanya bilangan cacah (integer), bilangan positip dan negatif, bilangan pecahan dan irrational, dan berbagai bilangan lain yang semuanya dikatakan sebagai bilangan riel. Lalu ada lagi bilangan yang tidak termasuk bilangan riel, yang dikenal sebagai bilangan khayal. Dinamakan bilangan khayal, karena memang keberadaannya hanya ada dalam khayalan, tentu dalam pemikiran matematika. Karena bilangan ini didefinisikan sebagai akar dari bilangan negatif.
Kalau dari segi operasi akar, maka dapat saja kita bilang: “Kenapa sih, kita tidak dapat menerapkan operasi akar terhadap bilangan negatif? Rasanya sebagai operator matematis, mestinya akar juga dapat diterapkan pada sembarang bilangan riel, baik positif ataupun negatif. Tapi nanti dulu! Apa sih, sebenarnya operasi akar itu? Kalau kita lihat ?4=2; ya, karena bila 2 dikwadratkan hasilnya sama dengan 4. Jadi akar secara gampangnya, adalah kebalikan dari operasi kwadrat. Lalu sekarang kita terapkan operasi kwadrat pada bilangan negatif; bisa saja misalnya (-2)2= 4. Lihat hasilnya, positip kan?.
Ternyata bilangan apapun baik positip maupun negatip kalau dikwadratkan hasilnya selalu positip. Tidak pernah ada hasil kwadrat yang negatip. Jadi kalau begitu, tidak mungkinkah kita mengambil akar dari suatu bilangan negatip? Yah, begitulah!
ADVERTISEMENT
SCROLL TO RESUME CONTENT
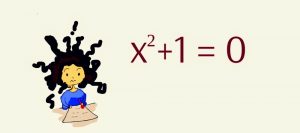Para matematikawan zaman dulu nampaknya puas dengan jawaban itu. Mau diapakan pun kita tidak akan dapat menerapkan operasi akar terhadap bilangan negatip. Tapi tidak demikian dengan Rafaello Bombelli, seorang matematikawan dari Italia yang hidup dalam abad ke-16. Ia menemukan bahwa dalam upaya mencari pemecahan aljabar akan banyak gunanya kalau kita boleh mengandaikan bahwa bilangan negatip dapat diakarkan. Dengan kata lain, kalau persamaan seperti x+ 1=0 dapat dicari solusinya dengan memberikan harga x=-1, maka persamaan x2 + 1 =0 mestinya dapat juga dipecahkan hanya dengan memberikan harga k=?-1.
Rasanya asumsi adanya akar dari bilangan -1, akan dapat menyederhanakan perhitungan tertentu, dan boleh saja asal pada akhirnya nanti dapat menghasilkan harga yang “nyata”. Sama saja dengan bilangan negatip. Kalau kita, misalnya saja, menghitung jumlah ayam yang ada dalam kandang. Untuk menghitung jumlahnya boleh saja kita menggunakan bilangan negatip, misalnya saja kemarin ada 150 ekor, lalu sekarang hanya 100 karena yang 50 ekor sudah dijual. Maka ayam yang ada dalam kandang 150 + (-50) = 100 ekor. Di sini kita menggunakan operasi dengan bilangan negatip, tapi hasilnya tetap saja “nyata” ada 100. Kita tidak akan dapat menyatakan ayam 150 ekor dijual yang 200 sehingga sisanya kurang 50 ekor, karena ayam negatip kan tidak ada? Tapi sebagai persamaan matematis tokh kita boleh menulis: 150-200= -50?
Sepanjang abad ke-17 dan 18 banyak matematikawan yang berusaha mencari cara untuk memanfaatkan akar bilangan negatip. Seorang di antaranya Leonard Euler dalam abad ke-18 mengenalkan simbol i (huruf pertama dari kata bahasa. Latin imaginarius) untuk bilangan ?-1, dan menamakannya “sebagai bilangan imajiner (khayal). Leibnitz menggambarkan bilangan khayal ini sebagai “Karunia Tuhan”, suatu bilangan amphibi, antara ada dan tiada. Sedangkan Euler sendiri mengatakan bilangan seperti itu bukannya tiada, lebih atau kurang dari tiada, tapi benar-benar ada hanya dalam khayalan serta tidak mungkin ada. Suatu kalimat yang membingungkan memang!.
Para matematikawan akhirnya memberlakukan suatu aturan aljabar baru yang meliputi pemanfaatan bilangan “khayal murni” yang kemudian berkembang menjadi bilangan kompleks, yaitu jumlah dari bilangan khayal dan nyata (riel). Suatu bilangan kompleks dapat dituliskan dalam bentuk a+bi, dimana a dan b adalah bilangan riel. Dalam hal ini tanda tambah (+) tidak menunjukkan operasi tambah yang biasa, melainkan hanya sebagai tanda untuk memisahkan bagian riel a, dari bagian bilangan khayalnya bi. Dengah kata lain, bila a=0, dan b tidak nol, maka bilangan kompleks tadi merupakan bilangan khayal murni, sebaliknya bila b=0 dan a tidak nol, merupakan bilangan riel. Jadi bilangan kompleks meliputi dua bagian kumpulan (subset) yang beranggotakan bilangan khayal dan bilangan riel, di mana bilangan a dan b nya meliputi semua bilangan riel, berupa bilangan cacah (integer), pecahan maupun bilangan bukan pecahan (irrational).
Medan Kompleks
Dalam terminologi modern, bilangan kompleks memiliki bentuk struktur matematis yang disebut medan, yang unsur-unsurnya mematuhi hukum-hukum aritmatika yang biasa. Medan bilangan kompleks juga merupakan medan tertutup yang mematuhi hukum operasi tambah, kurang, kali dan bagi. Artinya dengan menerapkan operasi tersebut terhadap dua atau lebih bilangan kompleks, akan menghasilkan bilangan lain dalam medan kompleks. Penemuan bilangan kompleks ini sangat menguntungkan dalam operasi aljabar, karena dengan demikian kita akan dapat memecahkan segala macam persamaan aljabar bagaimanapun bentuknya. Misalnya saja persamaan yang amat sederhana: x2+x+1=0, hanya dapat dicari jawabnya dengan adanya bilangan kompleks. Medan kompleks juga membuka cakrawala lebih luas dalam perhitungan kalkulus, dan lebih lanjut lagi menghasilkan adanya masalah baru dari teori fungsi, yaitu teori fungsi kompleks.
Perkembangan bilangan dan fungsi kompleks dalam zaman modern ini telah menyusup ke aplikasi matematis dalam banyak cabang ilmu. Banyak perhitungan dalam ilmu fisika zaman modern ini bahkan tak mungkin dilakukan tanpa menggunakan perhitungan dalam medan kompleks. Pemanfaatan bilangan kompleks untuk membantu perhitungan praktis, mula-mula dilakukan, oleh Charles Proteus Steinmetz. Ia menemukan betapa bergunanya konsep bilangan kompleks untuk melakukan perhitungan arus listrik bolak-balik. Sekarang ini tak ada insinyur listrik yang tidak menggunakan bilangan kompleks dalam perhitungannya, demikian juga mereka yang bekerja dengan masalah gerakan udara maupun dinamika fluida. Bilangan kompleks juga memegang peran amat penting dalam pengembangan teori relativitas, dalam mekanika kwantum dan berbagai cabang lain dari fisika modern.
Dengan semakin banyaknya dan bermanfaatnya bilangan khayal, maka banyak pihak yang mempertanyakan: masih tepatkah nama ’bilangan khayal’? Karena nyatanya bilangan ini “ada”, buktinya dapat digunakan untuk menghitung hal-hal yang benar-benar ada, seperti yang ditunjukkan oleh arus listrik, fisika kwantum dan lain-lain. Bilangan kompleks memiliki sifat seperti bilangan biasa bila ditambah, kurang, kali dan bagi, sehingga banyak matematikawan tidak lagi segan untuk menyebut dan memperlakukan bilangan kompleks sama “nyata”-nya ”seperti bilangan negatip.
Memang bilangan kompleks, juga bilangan negatip, selama ini hanya dianggap sebagai simbol saja untuk melakukan manipulasi matematis. Lalu bukankah bilangan riel juga hanya simbol? Kita berpikir tentang suatu bilangan yang lebih “nyata” dari bilangan lain hanya karena penggunaannya demikian dekatnya dengan pengalaman praktis ketika kita akan menghitung jari, ayam, rumah, orang dan lain-lain. Tapi kita lupa bahwa hanya jari, ayam, rumah serta orang itulah yang nyata, benar-benar ada, bukan simbol bilangan yang kita gambar untuk menghitungnya. Bukankah hitungan 2 ekor sapi misalnya, yang benar-benar nyata adalah sapinya? Dan 2 hanya sekedar simbol. Lalu apa bedanya dengan bilangan -2 maupun 2?-1?. Dalam kenyataan matematika murni, bilangan i jelas “ada” seperti juga bilangan 2. Bila perlu, kita dapat juga berpikir bahwa angka 2 tidak lebih dari suatu operator: simbol untuk menggandakan bilangan 1.
Tetapi kebanyakan kita sudah terlalu biasa dengan bilangan riel, yang memang “nyata” dan ada, sehingga sulit untuk menerima bilangan yang “tidak mungkip ada” menjadi “nyata”. Dengan pikiran seperti ini para matematikawan berusaha mencan intepretasi dari bilangan kompleks. Akhirya mereka menemukannya, yaitu interpretasi geometrik dari bilangan tersebut. Secara geometrik, kita dengan mudah dapat “melihat” apakah sebenarnya bilangan kompleks ini, yaitu dengan mengidentifikasikan setiap bilangan kompleks dengan suatu titik dalam bidang cartesian.
Metode ini mula-mula diperkenalkan oleh Caspar Wessel, seorang matematikawan otodidak (belajar sendiri tanpa guru), dari Norwegia. Ia mengemukakan metodenya dalam suatu ceramah matematika pada tahun 1797. Beberapa tahun kemudian idenya ditemukan kembali oleh seorang pemegang buku dari Swiss, Jean Robert Argund. Ia mengemukakan masalah ini dalam buku kecilnya yang diterbitkan pada tahun 1806. Dan secara terpisah matematikawan besar dari Jerman, Carl Friedrich Gauss, juga menemukan dan mengembangkan lebih jauh ide Casper Wessel tadi.
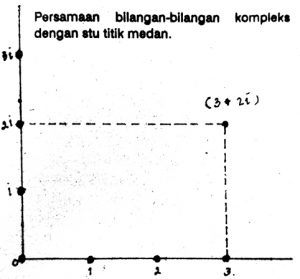
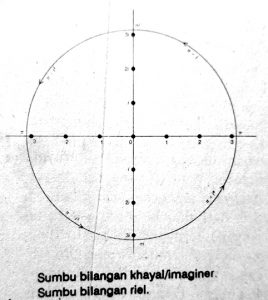
Ide dasar dari interpretasi geometri bilangan kompleks adalah dengan menggambarkan sumbu horizontal (X) sebagai garis bilangan riel, dan sumbu vertikal (Y) sebagai garis bilangan khayal (lihat gambar). Jadi bilangan 2+3i misalnya digambarkan sebagai titik yang memiliki absis (panjangnya pada sumbu X)2, dan ordinat (panjang pada sumbu Y) 3, dan seterusnya. Dengan cara ini kita dapat menggambarkan setiap bilangan kompleks. Setiap titik di sumbu X, berarti tidak memiliki faktor khayal, menggambarkan bilangan riel. Hal sebaliknya terjadi pada sumbu Y yang seluruhnya menggambarkan bilangan khayal.
Dengan interpretasi semacam ini, kita dapat melupakan sama sekali pengertian yang agak mengganggu, bahwa i adalah ?-1, suatu bilangan yang “tidak mungkin ada”. Sekarang suatu bilangan kompleks dapat dipandang sebagai suatu pasangan sederhana dari bilangan riel biasa: yang pertama menggambarkan panjangnya pada sumbu riel, dan kedua panjangnya pada sumbu khayal. Dengan kata lain, dengan mendefinisikan operasi aritmatik pada kombinasi pasangan ini, kita dapat membangun suatu operasi aljabar dari pasangan bilangan riel, yang sama dengan hukum aljabar yang berlaku dalam bilangan kompleks. Artinya dalam hal ini bahwa bilangan kompleks dapat disamakan dengan bilangan riel dengan dua dimensi.
Sama Dengan 8
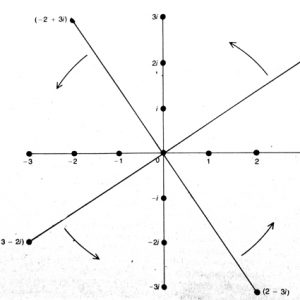
Karena adanya hubungan antara bilangan kompleks dan titik dalam bidang Cartesian, maka bidang ini juga disebut bidahg kompleks bila sedang digunakan untuk operasi bilangan kompleks. Untuk mengalikan suatu bilangan dalam bidang kompleks dengan i, maka kita mengambil garis radius vektor pada titik bilangan itu (yaitu garis dari titik asal ke titik bilangan dalam bidang kompleks) dan memutarnya 90o berlawanan arah jarum jam. Titik akhir dari garis baru ini merupakan hasil kali dari bilangan itu dengan i (lihat gambar).
Dalam hal seperti ini, kita melihat bahwa i dapat dianggap sebagai operator. Untuk dapat lebih mengerti ide ini, misalkan saja bahwa i dapat dipangkatkan berapa saja. Jadi i1=i; i2=-1 (karena i=?-1), i3=-i dan i4=1. Empat tahapan ini akan berulang lagi: : i5 =i, i6=-1, i7 =-i, i8=1 dan seterusnya. Setiap pangkat genap dari i menghasilkan -1 atau 1 sedang pangkat ganjil menghasilkan i atau –i.
Ilustrasi pada gambar (3), menggambarkan perkalian (dalam hal ini bilangan ?) dengan i. Titik yang berharga ? berada pada sumbu X; ketika dikalikan i, garisnya diputar berlawanan arah jarum jam sebesar 90o. Hasilnya berada di garis sumbu khayal, titik ini adalah titik ?i, demikian seterusnya ketika dikalikan i2, i3 dan i4 menghasilkan titik – ?, – ?i dan kembali ke ?.
Kebalikan operasi kali adalah operasi bagi. Untuk membagi suatu bilangan kompleks dengan i, tinggal memutar 90° searah jarum jam. Dengan hukum ini kita dapat melakukan “gurauan matematis”, yaitu bahwa “bilangan tak hingga kali i sama dengan 8”. Bagaimana mungkin? Coba saja anda buat simbol tak hingga (?), dikalikan i artinya tinggal memutar simbol ini berlawanan arah jarum jam sebesar 90°, akan anda dapatkan angka 8, bukan?
Dengan interpretasi perkalian semacam itu, .maka dapat disimpulkan bahwa bila akar kompleks dapat dihitung maka setiap bilangan tidak nol (baik riel maupun kompleks) memiliki tepat n buah akar ke n. Misalnya ?4 adalah 2 dan -2. Dengan kalimat sederhana, setiap bilangan memiliki dua akar kwadrat, 3 akar pangkat tiga dan seterusnya. Artinya setiap persamaan aljabar pangkat 3 harus punya 3 jawab, pangkat 4 punya 4 jawab dan seterusnya. Namun ketika kita menggambarkan akar dari suatlu bilangan dalam bidang komplek s, ternyata muncul hal-hal yang tidak terduga dan amat menarik. Semua n titik dari akar ke n dari suatu bilangan, ternyata di suatu lingkaran dan semuanya memiliki jarak yang satu sama lain di bidang kompleks. Dengan kata lain, titik akar pangkat n sebuah bilangan dalam bidang kompleks akan membentuk segi n beraturan. Contoh pada gambar 3, adalah akar pangkat 6 dari bilangan 729 atau 6?729, membentuk segi 6 beraturan seperti pada gambar.
Di samping manfaatnya yang besar dalam perhitungan ilmu fisika, konsep bilangan kompleks berkembang dengan sanggat menarik dalam teori bilangan. Sudah sejak lama orang tahu bahwa perkalian dua bilangan khayal akan menghasilkan bilangan nyata. Euler pada abad ke-18 menunjukkan bahwa i pangkat (ii) juga selalu riel, yang hasilnya sama dengan e-?/2 atau sama dengan sebuah bilangan irrational yang kalau dinyatakan dalam bilangan desimal menjadi 0,2078795762…. Bilangan e di sini adalah bilangan dasar logaritma natural. Sebenarnya bilangan ini hanyalah salah satu dari tak hingga banyak bilangan, semuanya riel, yang semuanya harganya sama dengan i pangkat i. Kumpulan bilangan ini memiliki rumus: e-?/2±2k?, dimana k adalah bilangan cacah (integer). Jadi bilangan irrational yang ditulis di atas adalah bilangan umum itu dengan k= 0. Sedangkan akar ke i dari i (i?i) juga bilangan riel, dengan harga utamanya (seperti tadi pada k=0), sama dengan e?/2 atau 4,8104773809…
Masih banyak lagi rumus yang menghubungkan i dengan dua buah bilangan irrational yang paling dikenal dalam matematika, yaitu bilangan e dan ?. Rumus yang paling terkanal adalah yang dikemukakan oleh Euler: ei?+1=0. Edward Kasner dan James Newman dalam bukunya Mathematics and the Imagination menggambarkan rumusan ini sebagai “jelas, singkat dan penuh arti”. Seorang matematikawan lain, Benjamin Peirce, suatu hari menyatakan tentang rumus ini: “Tuan-tuan, rumus ini memang benar, meskipun penuh pertentangan. Kita tidak dapat mengerti, tidak tahu apa artinya. Tapi kita telah membuktikannya, sehingga kita tahu bahwa itu .benar”. Tapi sebenarnya rumus itu memang bukan tanpa arti. Kalau kita tuliskan kembali sebagai: ei?=-1, maka kita dapat menggambarkannya dalam bidang kompleks sebagai limit dari suatu deret tak berhinga: 1 +?i+(?i)2/2! + (?i)3/3! + …. dimana n!=1x2x3x4x …… n. Deret ini dapat digambarkan sebagai suatu kumpulan tak hingga banyak titik pada suatu spiral berlawanan arah jarum jam dan suatu garis lurus yang berpusat di titik -1 pada sumbu riel. **(ma)
Sumber: Majalah Mekatronika, No. 76 –Juli 1089
