Delapan Halaman Surat Kabar untuk Menuliskan Bilangan Prima Terbesar

Pengumuman Perusahaan Riset Cray dari Amerika Serikat hari Senin, 10 Januari, mustinya menyentak penggemar matematika bilangan. Tim peneliti perusahaan ini berjaya menemukan bilangan prima yang dipercaya terbesar hingga saat ini. Bilangan berapakah itu? Harap bersabar. Tim Cray terpaksa menuliskan bilangan itu dengan notasi pangkat. Notasi ini tentu tak ada hubungannya dengan pangkat hirarkis seperti kolonel, jenderal atau lektor madya, profesor, atau bahkan buruh, majikan. Sungguh, matematika steril dari sistem hirarki yang berhubungan dengan gaji dan gengsi.

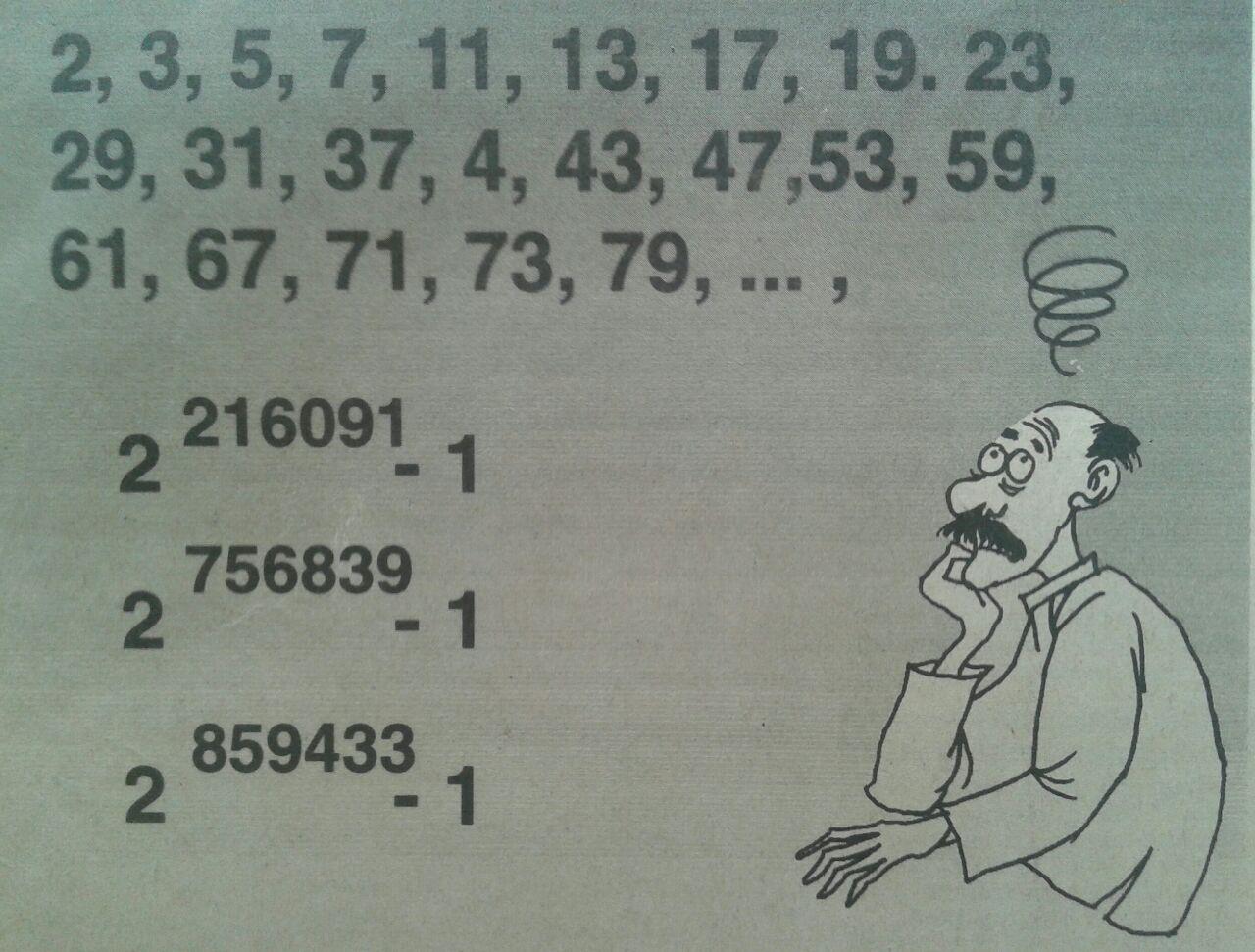
Perpangkatan dalam konteks ini adalah perkalian berulang. Lima pangkat tiga, yang ditulis sebagai 53, berarti bilangan 5 dikalikan dengan dirinya sendiri berulang sampai tiga kali. Jadi, 53 sama dengan 5 X 5 X 5. Nah, dengan notasi itulah tim Cray mengumumkan hasil kerja superkomputer mereka. Bilangan prima terbesar itu, kata mereka seperti diberitakan Reuters, adalah 2⁸⁵⁹⁴³³-1. Artinya, setelah 2 dipangkatkan dengan 859433, hasil perpangkatan itu dikurangi dengan 1. Tim Cray yang bermarkas di Eagan, Minnesota tentu saja tak bermaksud bersombong-sombong dengan notasi ini. Untuk diketahui, kalau 2⁸⁵⁹⁴³³-1 ditulis sebagaimana seribu ditulis dengan empat digit 1000, maka diperlukan delapan halaman surat kabar yang berisi angka sebesar huruf yang sedang Anda baca ini. Dengan kata lain, sebuah bilangan yang terdiri atas 258.716 digit.

Tentu tak bakal ada surat kabar yang berbaik hati mencuma-cumakan delapan halaman untuk menuliskan angka sebanyak itu. Bukankah ruang sebesar itu lebih baik dijual kepada pemasang iklan saja?

Notasi atau model, dalam matematika, sesungguhnya dibuat bukan untuk mempersukar. Seperti sebuah bahasa, ia justru mempermudah komunikasi. Lihat saja, 2⁸⁵⁹⁴³³-1 sudah cukup mewakili sebuah barisan angka yang menyita delapan halaman. Mustajab, bukan?

PERTANYAAN berikut dari kaum awam tentu saja: apakah bilangan prima itu?

Orang-orang sekolahan biasanya menjawab, bilangan prima adalah bilangan bulat positif dengan sifat khusus. Kalau kepadanya dilakukan operasi pembagian, hasil baginya hanya mungkin bilangan positif yang, kalau bukan dirinya sendiri, ya bilangan 1. Ke dalam kelompok inilah dimasukkan bilangan 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, dan seterusnya.

Semoga dengan contoh ini, lengkaplah pengertian tentang bilangan prima. Mudah menceknya. Untuk mendapatkan bilangan bulat, bilangan 7 hanya mempunyai pembagi 7 – yakni, dirinya sendiri – dan 1. Hasil pembagian dengan dirinya yang bulat itu adalah 1, hasil pembagian dengan 1, ya dirinya yang bulat positif itu pula. Bolak-balik jadinya, itulah istimewanya bilangan prima.

Bilangan prima penting diteliti sebab, hingga saat ini, belum ditemukan pola yang sistematis bila bilangan-bilangan itu dibariskan dari yang terkecil sampai yang “terbesar”. Rupanya, seperti halnya orang-orang ”istimewa” yang sukar diatur, bilangan prima dengan sifat istimewa itu sukar pula diatur.

Selain itu, untuk mencek apakah sebuah bilangan bulat positif masuk rumpun prima, setiap orang harus melakukan uji bagi dengan bilangan bulat positif yang lebih kecil daripada bilangan itu sendiri. Makin besar bilangan yang akan diuji, makin banyak pula uji coba yang dilakukan. Untuk mengetahui apakah bilangan 41 merupakan bilangan prima, setiap orang harus mencoba membaginya dengan bilangan bulat dari 1 sampai 41.

Itu sebabnya, selalu ada penghargaan pada setiap usaha menemukan bilangan prima terbesar dibandingkan bilangan prima terbesar yang pernah ditemukan orang pada saat tertentu. Kalaupun para penemu berbangga mengatakan ”itulah yang terbesar”, tentu saja pernyataan mereka tidak ditutup dengan titik sampai pada penggalan kalimat itu. Mengapa?
Euclid, matematikawan besar abad ketiga sebelum Masehi, pernah menulis sebuah proposisi pada salah satu jilid bukunya yang tersohor Stoichia Proposisi, yang dibuktikan dengan prosedur kontradiksi , memperlihatkan bahwa barisan bilangan prima – dalam bahasa matematika yang sangat serius- adalah tak berhingga. Dalam bahasa yang sederhana, barisan bilangan prima itu tak berujung. Karena itu, setiap penemuan bilangan prima terbesar selalu diimbuhi dengan kata hingga saat ini.

Satu misteri bilangan prima yang disisakan abad ke-17 terdapat dalam surat matematikawan Christian Goldbach (1690-1764) kepada Leonhard Euler (1707-1783) di tahun 1742. Kata Goldbach, setiap bilangan genap positif yang lebih besar daripada 2 selalu merupakan penjumlahan dua bilangan prima. Pernyataan Goldbach ini dinyatakan sebagai teorema tanpa bukti dalam buku Mediatationes Algebraicae karya Edward Waring (1734-1793) terbitan Inggris tahun 1770.

YANG pantas dicatat, kecepatan proses investigasi dengan mesin komputer membuat temuan bilangan prima yang kemudian makin cepat saja. Sukar dibayangkan, tanpa computer, ada orang yang bertekun-tekun mencari bilangan-bilangan prima caliber mahabesar, sampai enam digit.

Sebelum pengumuman tim Cray ini, yang terakhir adalah temuan kelompok Laboratorium Energi Atom Harwell, Oxfordshore, Inggris pada bulan Maret 1992. Ketika itu, mereka menemukan 2⁷⁵⁶⁸³⁹-1 sebagai bilangan prima terbesar dengan 227.832 digit yang menyita tujuh halaman surat kabar yang sedang Anda pegang (Kompas, 30 Maret 1992).

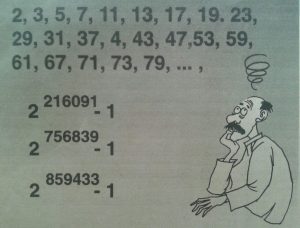Cepat bukan? Hanya dalam tempo 22 bulan sejak bilangan prima terbesar terakhir ditemukan Maret 1992, muncul bilangan prima terbesar tarbaru.

Sebelum temuan tim Harwell, bilangan prima 2²¹⁶⁰⁹¹-1 dengan 65.050 digit yang ditemukan ilmuwan dari Perusahaan teknologi Informasi Chevron, AS tahun 1985 bertahan hampri tujuh tahun sebagai yang terbesar.

Apa gunanya temuan ini?
Perusahaan riset Cray bilang, “Pada dasarnya usaha ini adalah untuk memuskan curiosity kami akan misteri bilangan prima.”

”Pokoknya tak ada pengaruhnya untuk menghitung bunga tabungan Anda di bank,” komentar Reuters dua tahun lalu ketika memberitakan temuan 2²¹⁶⁰⁹¹-1.

”Jangan buru-buru bilang tak berguna, toh bilangan kuaternion yang ketika ditemukan divonis tak berguna, nyatanya instrumental untuk menjelaskan fenomena kuantum. Jangan lupa, kuantum adalah ilmu dasar yang memajukan elektronika masa kini, dan komputer yang Anda dewa-dewakan itu,” tentu saja begini komentar fisikawan.

Orang yang sinis dengan kapitalis-kapitalis tulen, pasti akan bilang, temuan ini tentu sangat berarti bagi kapitalis manakala bilangan 2²¹⁶⁰⁹¹-1 itu disandingkan dengan kata rupiah atau dollar AS. Cukup membeli seluruh tanah di bumi manusia.
(Salomo Simanungkalit)

KOMPAS, MINGGU, 16 JANUARI 1994